The concept for an acceleration of public-key cryptanalysis methods

The Xilinx Zynq-7000 SoC provides new possibilities for increasing the efficiency of cryptanalysis methods for the public-key systems such as RSA or Diffie-Hellman key exchange algorithm. These cryptosystems are based on the discrete logarithm and integer factorization problem. After a brief introduction to numerical methods for solving these problems, there is an introduction to the distributed system that aims to solve these problems. A distributed system consists of master nodes that manage the distribution of the tasks and slave nodes that compute one of the most time-consuming parts of the selected numerical methods called sieving. Afterwards, the slave node is designed on Xilinx Zynq-7000 SoC consisting of an ARM processor for analyzing the problem and some custom IP cores running on FPGA to increase the algorithm's efficiency. The capabilities of the distributed system are also measured and analyzed afterwards.

Introduction

With the increasing computational potential of FPGA and the new approach of designing the specialized hardware, the security of public-key cryptosystems arises. This paper aims to analyze the possibilities of Xilinx Zynq-7000 SoC in solving integer factorization and discrete logarithm problems. It means it explores its potential on implementation of cryptanalysis methods for solving of mentioned problems.

Security of public-key cryptosystems

There are many cyphers and protocols in a branch of public-key cryptography. But only methods based on the principle of simple integer factorization and discrete logarithm are relevant in this paper.

Integer factorization problem

An example of a cypher based on the principle of integer factorization problem is RSA cryptosystem that uses public-key n of format n = pq for some large prime numbers p and q and some integer e such that e ∤ φ(n), where φ(n) represents Euler's totient function. The security of this cypher is based on the toughness of finding numbers p and q for given number n that could be afterwards used to compute φ(n) and the value of private key d.

In general, integer factorization problem could be defined as searching for the decomposition of given positive integer n to the following format:

n = Π_{i = 1}^r p_i^a_i

Where p_i is a prime number and a_i is a natural number (for each i = 1,2, ... ,r).

There are no known effective algorithms for solving this problem in polynomial time (except Shor's algorithm for quantum computers). The best-known algorithms for solving the integer factorization problem for large integers are:

• Quadratic Sieve - for integers of size less than approximately 10¹⁰⁰.
• General Number Field Sieve - for integers of length greater than approximately 10¹⁰⁰.

Discrete logarithm problem

The security of public-key cryptosystems could also be based on the discrete logarithm problem. For example, suppose that there is prime number p and the primitive root mod p - integer g and the random integer number a ∈ ℤ_p. Then, the discrete logarithm problem is searching for the value of integer k in the following congruence:

g^k ≡ a mod p

There is no known effective algorithm (except Shor's algorithm for quantum computers). Therefore, numerical methods for solving this problem are usually based on a combination of the following methods:

• Pohlig-Hellman algorithm: that could simplify the congruence.
• Index Calculus is the standard method (and the most effective one) for solving a discrete logarithm problem.

The well-known public-key protocol based on this principle is Diffie-Hellman key exchange.

Other approaches in public-key cryptography

There are also many other public-key cryptosystems based on different principles. Especially the elliptic curve cryptography is well known. Many quantum-resistant algorithms based on some NP-complete problems are also available. Numerical methods for cryptanalysis of these algorithms are not the subject of this paper.

A practical approach in cryptanalysis

The only way how to succeed in solving some real cryptanalysis integer factorization or discrete logarithm problem is to use some of the mentioned numerical methods and parallel approaches for this purpose. The possibility of using the FPGA for accelerating some parts of mentioned numerical methods is discussed below.

The parallel approach in integer factorization problem

Each of the currently used methods for integer factorization is similar to (or based on) Dixon's Random Square Method. This method consists of two steps; the first one is called sieving the other is called matrix processing. Each of these steps could be distributed for many computational nodes.

The sieving part of the algorithm consists of searching for some smooth integers over some factor base F (that usually contains prime numbers, most typically, first |F| prime numbers). The method tries to find a set of integers x_i such that n^0.5 ≤ x_i ≤ n and the value (x_i² mod n) is smooth over a set F. It means that there exists the following decomposition:

x_i² mod n = Π_{pj ∈ F, eij ∈ ℤ⁺} p_j^e_ij

The algorithm has to find at least (|F| + 1) of such integers x_i. This process could be easily distributed to as many nodes as possible. Each node generates the random value x_i and checks the smoothness of x_i over the factor base F. Other algorithms (especially General Number Field Sieve and Quadratic Sieve) have a sieving part equivalent to the represented ones. The sieving part of the algorithm is usually the slower one, and it is susceptible to selecting the correct value of the method's parameters.

The matrix processing part of the algorithm consists of computing the null space of a matrix of the exponents e_ij found in step over finite ℤ₂ field (because only the parity of exponents is relevant). Because of the sparsity of the given matrix, the block Lanczos algorithm could be used in this process as the most effective serial (single node) option. The size of the matrix in the realistic example is about 10⁶ rows and columns (for n > 2⁵¹²). The other method for computing the null space of a sparse matrix is the Wiedemann algorithm, which could be distributed to many computational nodes.

After the matrix processing part, the values of integers x and y are found such that:

x² ≡ y² mod n ∧ x ≢ ± y mod n

The value GCD(x ± y, n) could be a non-trivial divider of a given composed integer n.

The parallel approach in discrete logarithm problem

The Pohlig-Hellman algorithm contains the step in which the value (p - 1) is factorized (usually using some of the mentioned methods). In fact, the Pohling-Hellman algorithm could only be helpful when dealing with special cases, usually in case of security errors during implementation (like improperly selected keys).

Index Calculus method is the universal one. It also contains the sieving part and the matrix processing part. The sieving part is the same as the sieving part of Dixon's factorization method. The algorithm works with factor base F (usually composed of first |F| prime numbers) and checks the smoothness of values (g^x_i mod p) over factor base F (for some random integer x_i ∈ ℤ_{p - 1}). For example, the value could be expressed in the following way:

g^x_i mod p = Π_{pj ∈ F, eij ∈ ℤ⁺} p_j^e_ij

This part of the algorithm could be easily distributed to many nodes, which is similar to the sieving part of the integer factorization problem methods. First, index calculus has to find the set of integers x_i of cardinality |F| such that the matrix composed of exponents e_ij that fits the equation above is regular in the ℤ_{p - 1} ring.

The matrix processing part of the Index Calculus algorithm differs significantly. The most significant difference is that it works on ring ℤ_φ(p (where φ(p)=p - 1 is the value of Euler's totient function of prime number p). Unfortunately, this ring is not the field as the value p - 1 is always a composite number for large primes (in opposite to ℤ₂) which means that there is no effective algorithm for solving this equation set. Practically, only a variation of the Gaussian elimination can be used in this situation.

Improvements of considered algorithms

There is also a possibility of improvement of a particular numerical method itself. Many enhancements of each numerical method have been presented since 1990. It leads to an increase in the efficiency of each method. The most remarkable improvement has been noticed in the GNFS method (because it is the only effective method for larger integers). The most critical improvement (relatively to this paper) has been achieved in selecting a polynomial for the GNFS method. The runtime of methods depends especially on the choice of good polynomial pairs. Another essential part of the GNFS method is computing the square root value, which has also been improved.

The design of a distributed system

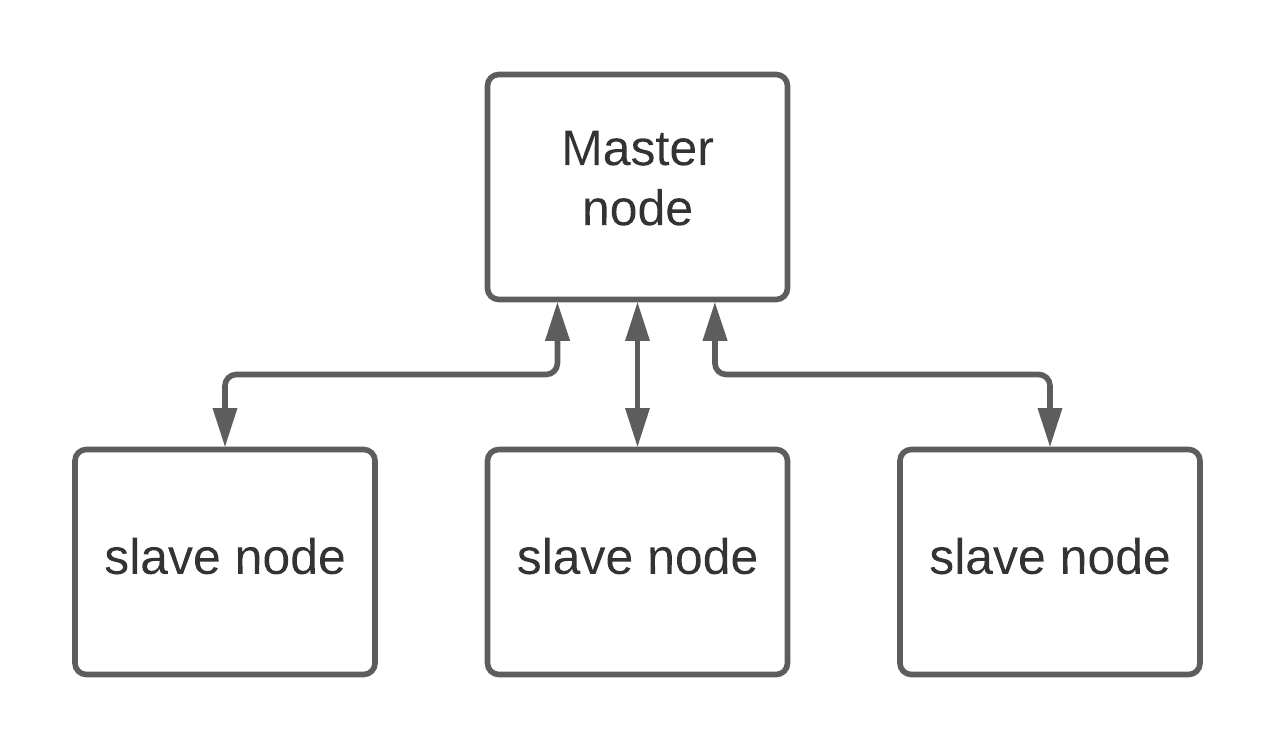
The distributed system has been designed to improve the sieving part of the General number field sieve algorithm and other methods (especially Index Calculus). It is composed of one master node that distributes the task to each slave node used for computing.

The master nod

The principal purpose of master node is specified in the following enumeration:

• Analyze of given cryptanalysis problem.
• Preprocessing of the assigned task and computing of the parameters of selected numerical methods.
• Managing the network of slave nodes.
• Postprocessing, especially the matrix processing problem.
• Representing of the results in some acceptable form.

The system has to analyze whether the given problem fits some pattern. Especially whether given number n that should be factorized is an odd composed number that is not k-smooth for some relatively small value of k or whether given modulus p in discrete logarithm problem is a prime number and the generator g is a primitive root mod p.

Pre-processing of input is another crucial part of the algorithm. For example, the discrete logarithm analysis contains the factorization of (p - 1) that could be used in the Pohlig-Hellman algorithm. Moreover, the computation of all other parameters of numerical methods is an essential part of this step. It includes finding the suitable composition of each factor base (rational factor base is composed of prime numbers, and in the case of GNFS method, there is also algebraic factor base with similar composition) and other relevant parameters (for example, searching for proper value coefficients of the polynomial in GNFS method).

Another important function of the master node is to handle network communication. It consists of distributing current tasks and parameters of numerical methods. A master node also has to fetch computed values (smooth over the given factor base) from slave nodes, check them and save them for the matrix processing part.

A master node also implements Montgomery's block Lanczos algorithm for computing of null space of found matrix over the ℤ₂ field (in case of the integer factorization problem) and Gaussian elimination method over ℤ_{p - 1} ring (in case of the discrete logarithm problem). After the sequence of computations, it also has to verify computed results (and skip or repeat some previous steps if the result is wrong).

Last but not least function of the master node is to save found values or represent results in some human-readable form.

The slave nod

The most crucial feature of slave node is to compute values of the sieving process. This process is slightly different in each numerical method:

• Quadratic Sieve: method works with factor base of the form ({n mod p / p} = 1 for each p ∈ F (where {a / p} is a Legendre symbol) and computes the smoothness of x_i inversely from p ∈ F using Tonelli-Shanks algorithm.
• GNFS: method works with three different factor bases called algebraic factor base (composed of first degree prime ideals in integer pair representation), rational factor base (consisting of prime numbers), and quadratic characteristic factor base (to verify smoothness). Slave node computes only values that are smooth over rational and algebraic factor base. Quadratic characteristic values are calculated afterwards separately.
• Index Calculus: method works with standard factor base composed of prime numbers.

This process requires the fast generator of random numbers and some fast algorithm for computing reminders after dividing the given random number and the prime number in the factor base. Another essential feature of the algorithm is effective working with large numbers (typically bigger than 10¹⁰⁰).

Another essential feature of slave node is periodically fetching commands from a master node and sending results back to master nod.

The FPGA approach

The suitable way for implementation of the slave node is to use Zynq-7000 SoC. It contains an ARM-based processor with programmable FPGA. Program running on processor implements the interface for communication with a master node and manages custom IP cores' properties. The IP cores created on FPGA implement the functionality relevant for the selected method. There are the following relevant IP cores in the system:

• Random number generator IP: generates relevant random numbers and checks their properties (for example, the GNFS method operates with two coprime numbers, while other methods operate with one random integer in some interval).
• Rational smoothness checking IP: that verifies whether a given integer is smooth over some factor base, consists of integers (rational factor base in GNFS method).
• Algebraic smoothness checking IP: checks whether an input is smooth over some algebraic factor base (only GNFS operates with this concept).

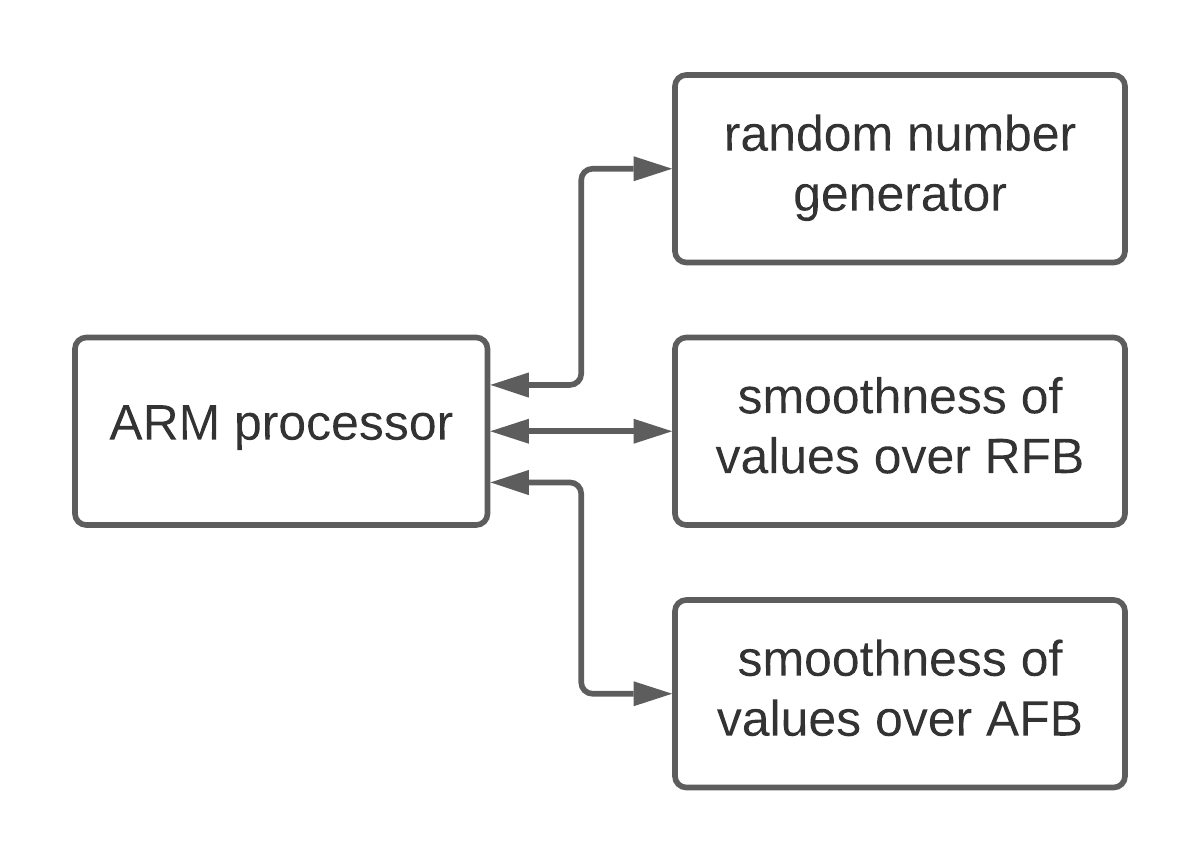
The scheme in the picture above is simplified, but it presents the principle aptly. Many other cores are practically used in the system (for example, the core for ethernet communication).

Rational smoothness checking on FPGA has been the subject of many improvements. For example, there is a possibility of checking whether the given input is k-smooth for some relatively small integer k using the Elliptic Curve Method that has already been implemented on FPGA.

Results of measurement

After the implementation of the distributed system, the measurement of its features has been performed.

Integer factorization problem

It is reasonable to presume that the dependency of numbers of nodes (slaves) in the system and the time required for solving the task is approximately (T₀ / S) where T₀ is the time required by a single node and S is the number of nodes connected to the system. By using exponential regression following pattern for computing of T₀ has been found:

T₀ = 0.31 · 10^-3 · exp(0.05 · N)

Where N represents the bit size of the input (T₀ in seconds), measured results are shown in the graph below.

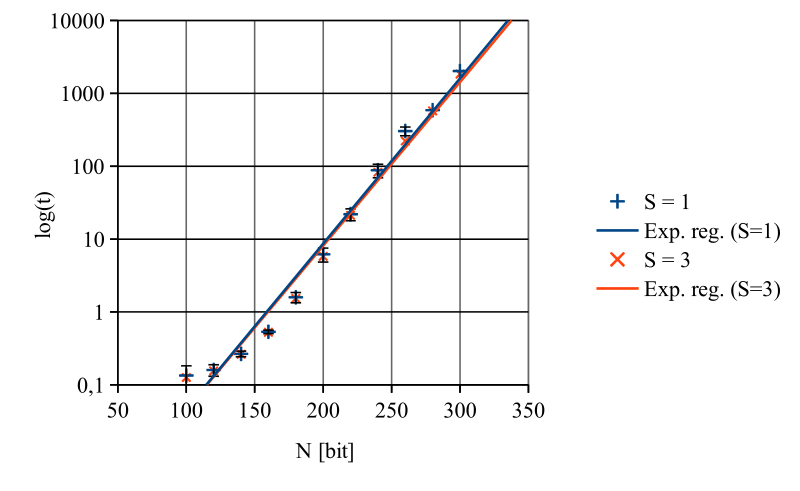
The presumption of dependency of numbers of nodes (slaves) in the system and the time required for solving the task has also been confirmed (t = T₀ / S).

Discrete logarithm problem

Methods for solving the discrete logarithm problem are less effective than the methods for solving the integer factorization problem. This leads to working with input of size smaller than in previous measurements. However, general presumptions, if it comes to vertical scalability, are the same as above.

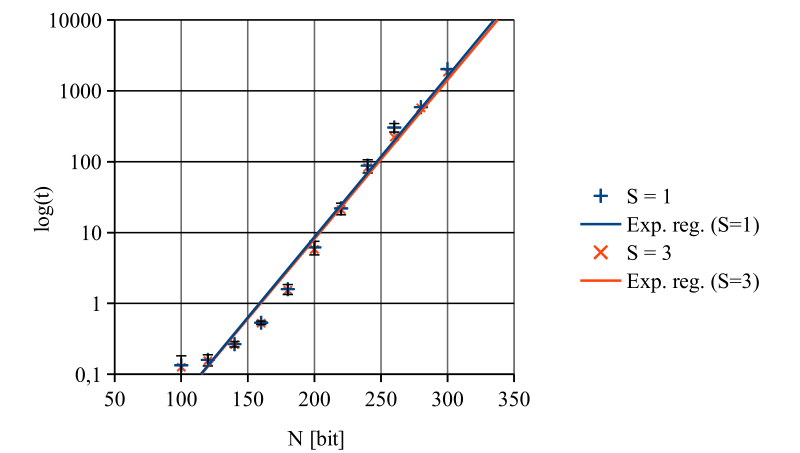
Exponential regression of measured values returns the following result:

T₀ = 8.85 · 10^-7 · exp(0.38 · N)

Where N represents the bit size of the input (T₀ in seconds). The presumption of dependency of numbers of nodes (slaves) in the system and the time required for solving the task has also been confirmed as t = T₀ / S.

Conclusions

This paper represents the possibilities of Zynq-7000 SoC in the cryptanalysis of the integer factorization problem and discrete logarithm problem-based cryptosystems. It has been shown that using custom IP cores could accelerate the sieving part of modern numeric methods for solving these problems. The sieving unit (or the slave node of a distributed system) comprises four major components: the random number generator IP, the IP for checking smoothness over rational factor base and algebraic factor base, and the ARM processor for managing the process. The paper also discussed the possibilities of a parallel approach in this process and other improvements of used numerical methods for solving integer factorization and discrete logarithm. The measurement shows that the relation between the bit size of the input and the time for sieving is almost exponential (that had been presumed). On the other hand, the relation between the number of nodes in the system and time spent for sieving is linear (also had been assumed).

References

[1] L. H. Crockett, R. A. Elliot, M. A. Enderwitz and R. W. Stewart, The Zynq Book, Strathclyde Academic Media, 2014, pp. 1-46. ISBN: 978- 0992978709
[2] H. Delfs and H. Knebl, Introduction to Cryptography, 3rd ed. Springer, Berlin, Heidelberg, 2015, pp. 49-112. doi: 10.1007/978-3-662-47974-2
[3] V. P. Hoang, Integer factorization with the general number field sieve, Rovaniemi University of Applied Sciences, 2008, pp. 39-58. ISBN: 978- 952-5153-78-1
[4] G. d. Meulenaer, F. Gosset, G. M. d. Dormale and J. J. Quisquater, ”Integer Factorization Based on Elliptic Curve Method: Towards Better Exploitation of Reconfigurable Hardware”, doi: 10.1109/FCCM.2007.12
[5] P. Nguyen, ”A Montgomery-like square root for the Number Field Sieve”, Buhler J.P. (eds) Algorithmic Number Theory. ANTS 1998. Lec- ture Notes in Computer Science, Vol. 1423. Springer, Berlin, Heidelberg
[6] I. Niven, An Introduction to the Theory of Numbers, 5th ed. Wiley, 1991, pp. 110-115. ISBN: 0-471-62546-9
[7] G. Pandey and S. K. Pal, ”Polynomial selection in number field sieve for integer factorization”, Perspectives in Science, Vol. 8, 2016, pp. 101-103, doi: 10.1016/j.pisc.2016.04.007.
[8] Y. Y. Song, 2017, Computational Number Theory and Modern Cryptography, Higher Education Press, 2017, pp. 191-260. doi: 10.1002/9781118188606.ch5
[9] L. T. Yang, Ying Huang, J. Feng, Q. Pan and C. Zhu, ”An improved parallel block Lanczos algorithm over GF(2) for integer factorization”, Information Sciences, doi: 10.1016/j.ins.2016.09.052.
[10] L. T. Yang, G. Huang, J. Feng and L. Xu, ”Parallel GNFS algorithm integrated with parallel block Wiedemann algorithm for RSA security in cloud computing”, Information Sciences, doi: 10.1016/j.ins.2016.10.017.

❋ Tags: Security FPGA Hardware Design Cryptosystem